Examples of sets include the set of integers, the set of natural numbers, the set of real numbers, and the empty set. More specifically, the set of integers contains numbers such as -2, -1, 0, 1, 2, and so on. The set of natural numbers contains the numbers 1, 2, 3, and so forth. The set of real numbers includes integers, fractions, irrational numbers like π, and so on.
- Examples of Sets
- 1. Set of Scores in a Game
- 2. Set of Food Orders at a Restaurant
- 3. Set of Student Test Scores
- 4. Set of Gene Variations in Biology
- 5. Set of Weather Readings
- 6. Set of Shapes in Geometry Proofs
- 7. Set of Even and Odd Numbers
- 8. Set of Airline Flight Numbers
- 9. Set of Contest Participant Entries
- 10. Set of Prices in Economic Theory
Examples of Sets
Here are 10 real world examples of sets in math:
1. Set of Scores in a Game
The collection of all the possible numerical final scores that can be achieved by players in a particular game forms the set of scores. It includes repeated instances of the same scores attained by multiple players. The elements are related by being scores in that game.
- Roster form: {0, 1, 2, 3, …, maximum score possible in the game}
- Set-builder form: {x | x is a possible score in the game}

2. Set of Food Orders at a Restaurant
The food items ordered by all customers across all tables during each day make up the elements of the daily order set. Though dishes repeat frequently, each order instance is distinct, so order sets grow very large over years. Menus may change but every dish served ever can define the total historical order set.
- Roster form: {pizza, burger, fries, salad, …, all items on the menu}
- Set-builder form: {x | x is a food item ordered by a customer}

3. Set of Student Test Scores
The set contains percentage test scores from 0-100% attained by every individual student on a particular exam. Score groupings emerge for classes, grades, demographics etc. Possible scores exist on a defined range so the score set has a logical maximum and minimum bound.
- Roster form: {0, 1, 2, …, 100} (assuming scores are out of 100)
- Set-builder form: {x | x is a test score attained by a student}

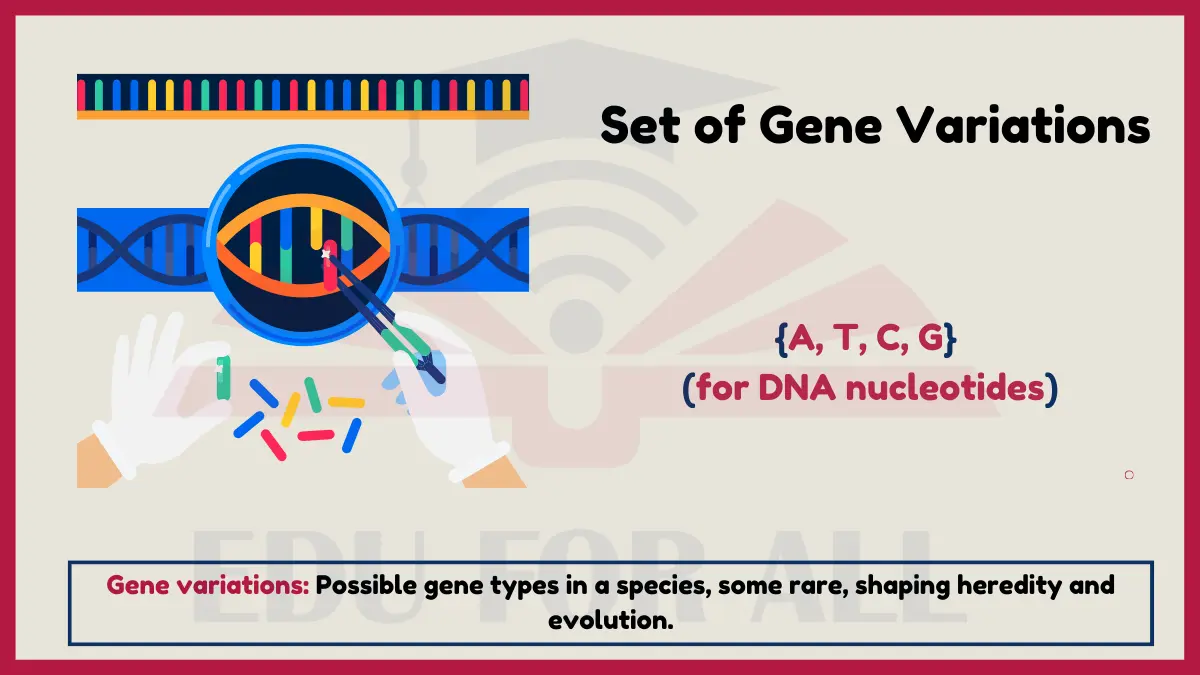
4. Set of Gene Variations in Biology
All possible alternative gene types (alleles) that can occur for a gene locus in a species breeding population constitute that species’ allele set for the target gene. Some alleles may be common while others are rare in the set.
- Roster form: {A, T, C, G} (for DNA nucleotides)
- Set-builder form: {a | a is a possible allele for the gene}
5. Set of Weather Readings
Historical data measurements of weather elements like daily minimum and maximum temperatures or precipitation are individual set elements. Ranges depend on instrumentation precision but allow finescale trend analysis when the set grows large enough.
- Roster form: {(date1, temperature1, rainfall1), (date2, temperature2, rainfall2), …}
- Set-builder form: {(date, temperature, rainfall) | date is a day on which measurements were taken}

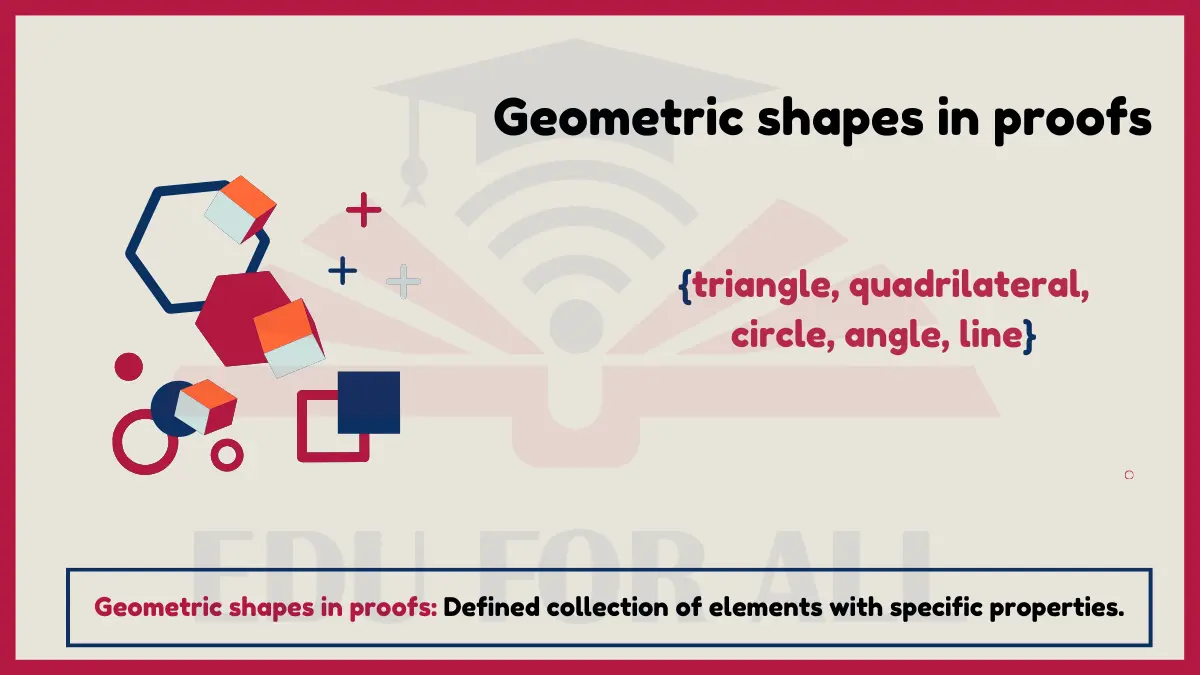
6. Set of Shapes in Geometry Proofs
When conducting geometric proofs, the set of geometric shapes under consideration contains elements like triangles, quadrilaterals, regular polygons, circles, angles and lines that hold certain defined properties. These properties may constrain shapes to right angles, congruence, arbitrary size etc. New elements can be derived by combining existing shapes via operations of intersection, exclusion etc.
- Roster form: {triangle, quadrilateral, circle, angle, line}
- Set-builder form: {s | s is a shape involved in the geometric proof}
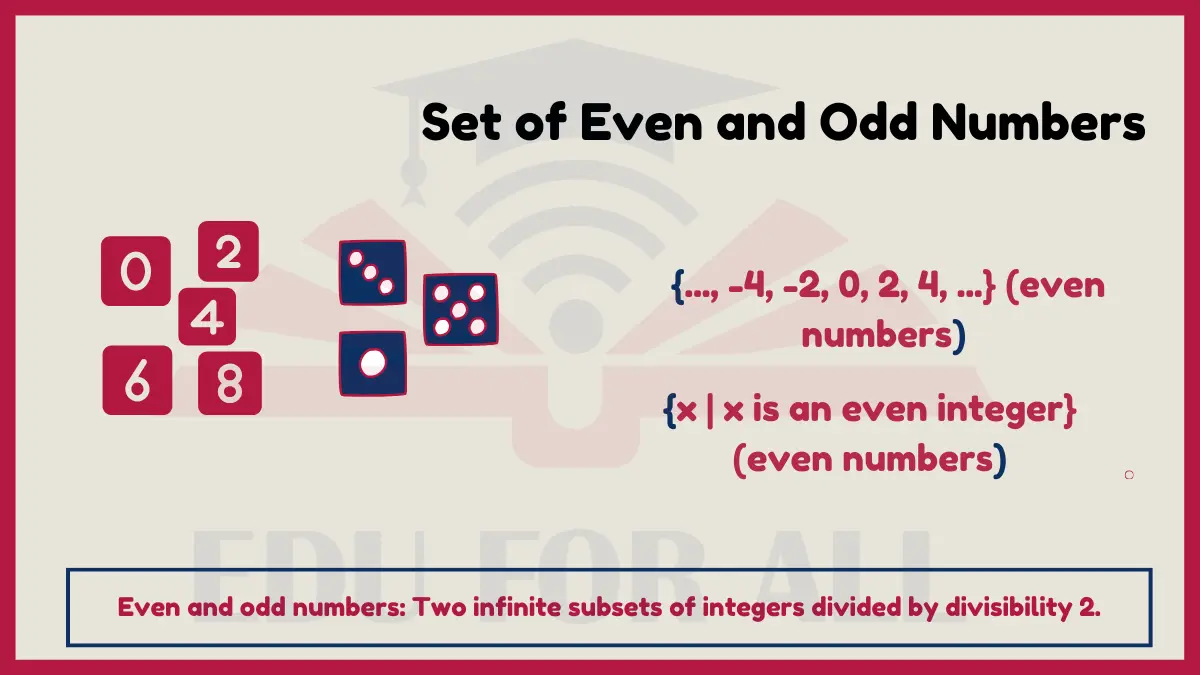
7. Set of Even and Odd Numbers
The set of integers can be divided into two distinct infinite subsets – the set of even numbers containing elements exactly divisible by 2, and the set of odd numbers, with elements not divisible by 2. Defining properties of parity determine categorization into one set or the other, with no numbers belonging to both.
- Roster form: {…, -4, -2, 0, 2, 4, …} (even numbers)
- Roster form: {…, -3, -1, 1, 3, …} (odd numbers)
- Set-builder form: {x | x is an even integer} (even numbers)
- Set-builder form: {x | x is an odd integer} (odd numbers)
8. Set of Airline Flight Numbers
Every commercial flight is assigned a unique flight number consisting of a combination of digits and letters according to specific airline conventions. The total collection of current flight numbers designating active routes constitutes the airline’s master flight number set at a snapshot in time.
- Roster form: {flight number 1, flight number 2, …, flight number N}
- Set-builder form: {x | x is a flight number assigned by the airline}
9. Set of Contest Participant Entries
In innovation challenges and design competitions, the collection of all entries submitted forms a set where individual entries represent distinct elements numbered in the thousands. Though containing similarities, each concept or creative work constitutes a unique element with measurable variation.
- Roster form: {entry1, entry2, …, entry N}
- Set-builder form: {x | x is a submitted entry for the contest}
10. Set of Prices in Economic Theory
The set of all possible prices that can exist for different goods and services available to consumers forms the overall price set within an economic system. Prices cluster around market equilibriums. Distributions vary by industry and change dynamically according to economic factors.
- Roster form: {p | p is a possible price for a good or service}

