Intersecting lines are two or more lines that cross or meet at a point. The intersection forms angles and line segments that can be analyzed using geometry and trigonometry.
Two arms of a cross, sides of a square door, edges of a book, railway tracks and platform, lines on a sheet of music, lines on a highway, streets in a grid pattern, railway tracks and crosswalk, arms of a pair of scissors, spokes of a bicycle wheel, diagonals of a rectangle, lines of a road intersection, lines of a kite, lines of a trapezoid, branches of a tree, and veins in a leaf are few examples of intersecting lines.
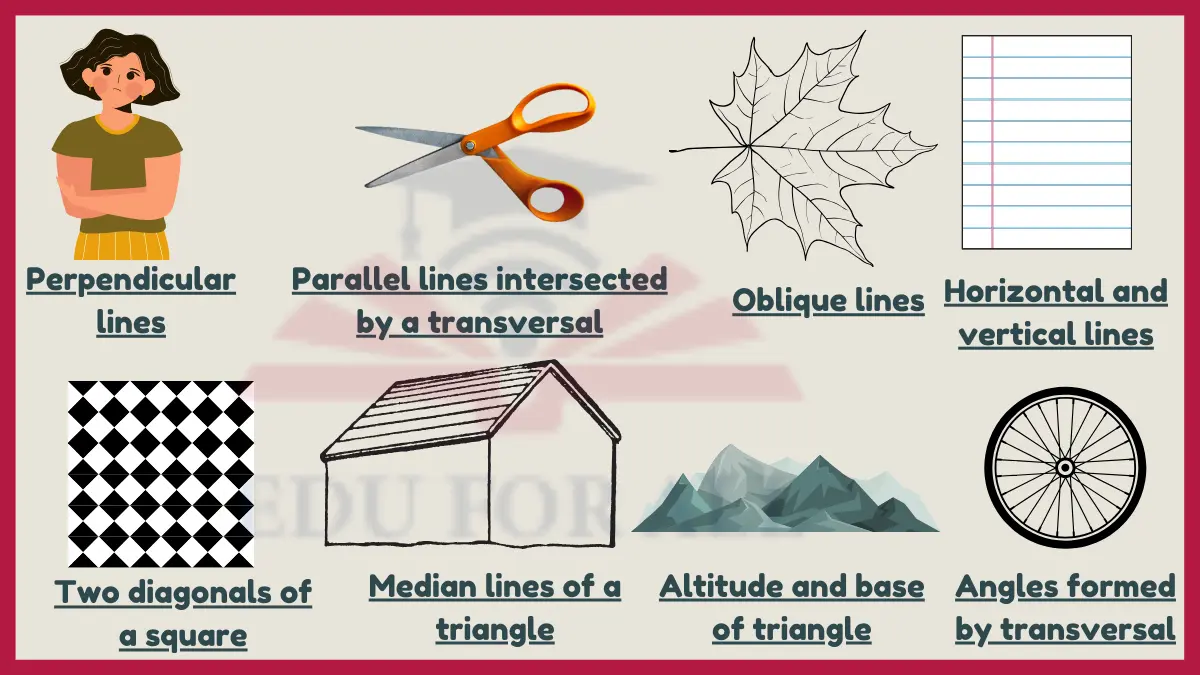
Examples of Intersecting Lines
Here are 10 examples of intersecting lines with examples:
1. Perpendicular lines
Perpendicular lines intersect at right angles (90° angles). Their slopes are negative reciprocals of each other.
Examples:
- The two arms of a cross
- The sides of a square door
- The edges of a book
- The railway tracks and the platform at a train station
- The lines on a sheet of music
2. Parallel lines intersected by a transversal
Parallel lines crossed by a transversal line create corresponding angles and proportional segments.
Examples:
- The lines on a highway
- The streets in a grid pattern
- The railway tracks and the crosswalk
- The arms of a pair of scissors
- The spokes of a bicycle wheel
3. Oblique lines
Oblique lines intersect at angles that are not 90° or 180°. Their intersection forms acute and obtuse angles.
Examples:
- The diagonals of a rectangle
- The lines of a road intersection
- The lines of a kite
- The lines of a trapezoid
- The branches of a tree
- The veins in a leaf
4. Horizontal and vertical lines
Horizontal and vertical lines intersect to form right angles at their intersection point. They are perpendicular to each other.
Examples:
Horizontal lines:
- The waterline on a beach
- The line between the sky and the ground
- The lines on a sheet of paper
- The lines on a computer screen
- The lines on a road
Vertical lines:
- The sides of a door
- The edges of a book
- The trunks of trees
- The poles of a power line
- The lines on a ruler
5. Two diagonals of a square
The diagonals of a square intersect perpendicularly at the center point andbisect each other into two equal line segments.
Examples:
- The diagonals of a chessboard
- The diagonals of a square tile
- The diagonals of a square window
- The diagonals of a square table
6. Median lines of triangle
The three median lines of a triangle intersect at the centroid, dividing each median in a 2:1 ratio.
Examples:
- The median lines of a traffic triangle
- The median lines of a triangular roof
- The median lines of a triangular sail
- The median lines of a triangular flower bed
7. Altitude and base of triangle
The two diagonals of a square intersect perpendicularly at the center point of the square, and they bisect each other into two equal line segments. This means that each diagonal cuts the other diagonal in half.
Examples:
- The height of a mountain
- The height of a building
- The height of a tree
- The height of a flagpole
- The height of a ramp
8. Angles formed by a transversal
When a transversal intersects two parallel lines, it creates corresponding angles and alternate interior angles. Corresponding angles are angles that are located in the same position relative to the two lines. Alternate interior angles are angles that are located inside the two parallel lines on opposite sides of the transversal. Corresponding angles and alternate interior angles are congruent, meaning that they have the same measure.
Examples:
- The angles formed by a railway track crossing a road
- The angles formed by a power line crossing a street
- The angles formed by a crosswalk crossing a street
- The angles formed by the arms of a pair of scissors crossing each other
- The angles formed by the spokes of a bicycle wheel crossing each other
9. Railway tracks
Straight railway tracks that intersect have switches that allow trains to transfer from one track to another. Switches are movable sections of track that can be moved to direct trains to different tracks.
Examples:
- The intersection of two railway tracks at a train station
- The intersection of two railway tracks at a junction
- The intersection of two railway tracks at a crossing
- The intersection of two railway tracks in a depot
10. X- and Y-axes on a graph
The X- and Y-axes on a 2D Cartesian coordinate plane intersect perpendicularly at the origin point (0, 0). The origin point is the point where the two axes cross.
Examples:
- A graph showing the relationship between the temperature of a city and the time of day
- A graph showing the relationship between the number of hours studied and the exam score
- A graph showing the relationship between the price of a product and the quantity sold
- A graph showing the relationship between the height of a plant and the amount of water it receives
Also Read





