From rectangular pizza boxes to circular basketball courts, area is everywhere. We can measure the surface covered by any shape, like the square of a backyard playing field or the triangle of a slice of pie. To do this, we use different formulas based on the shapes, like multiplying length and width for rectangles or using π and the radius for circles.
Examples of Area
Here are some Examples of Area in math:
1. Rectangle Area
The area of a rectangle is calculated by multiplying its length and width. For example, if a rectangle has a length of 5 units and a width of 3 units, its area would be 5 x 3 = 15 square units.

Used to determine the amount of paint needed for a rectangular wall.
Experiment: Take a rectangular piece of paper and use a ruler to carefully measure its length and width. Multiply the length and the width that you measured to calculate the total area of the rectangle.
2. Circle Area
The area of a circle can be found by using the formula: Area = π x (radius)2. For example, if a circle has a radius of 2 units, first square the radius (2 x 2 = 4) and then multiply it by π, so the area would be 4 x π square units.
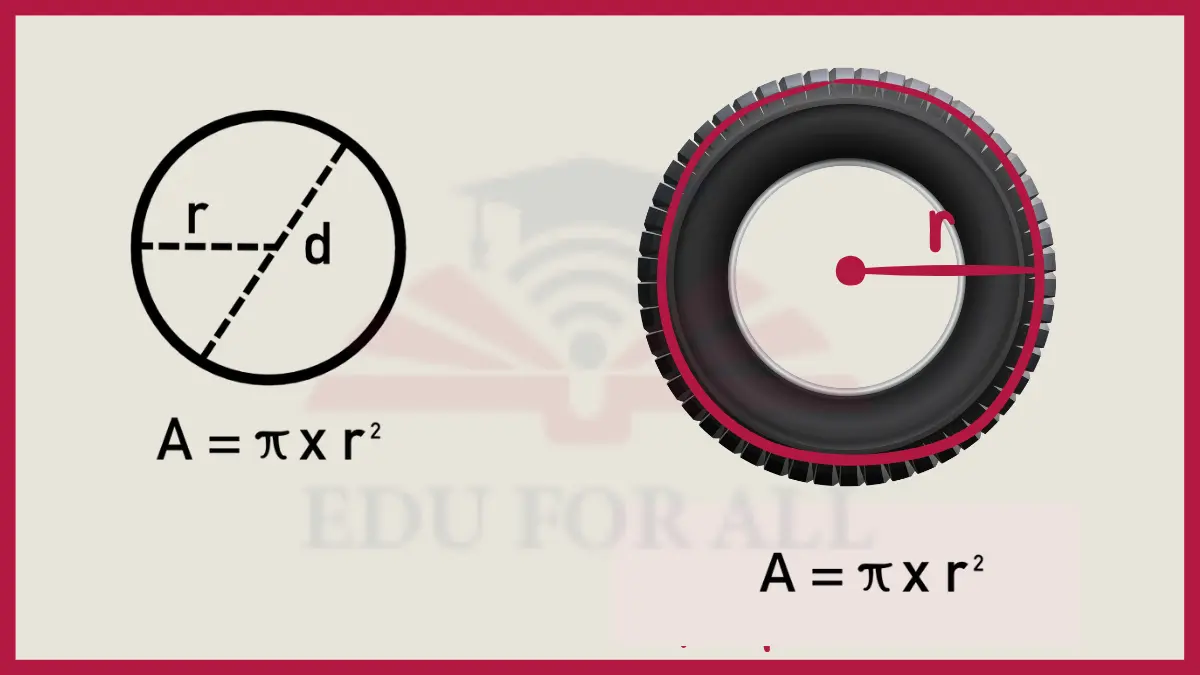
Used to determine the space required for a circular swimming pool.
Experiment: Use a piece of string to measure the radius or distance from the center of a circular object to its edge. Square this radius measurement and multiply it by 3.14 (or use the π button on a calculator) to find the circle’s total area.
3. Triangle Area
To find the area of a triangle, you use the formula: Area = 1/2 x base x height. For example, if a triangle has a base of 6 units and a height of 4 units, then the area would be 1/2 x 6 x 4 = 12 square units.

Used to determine the amount of fabric needed for a triangular flag.
Experiment: Draw a triangle on a sheet of paper. Using a ruler, measure the length of its base. Then draw in the height by making a line from the opposite corner perpendicular (at a 90 degree angle) to the base. Measure this height. Multiply the base and height measurements together, divide by 2, and you have found the total area!
4. Trapezoid Area
The area of a trapezoid is found by taking the average of the two bases, multiplying that by the height: Area = (Base 1 + Base 2) /2 x Height. For example, a trapezoid with bases of 8 units and 12 units, and a height of 5 units, would have an area of (8 + 12) / 2 x 5 = 50 square units.
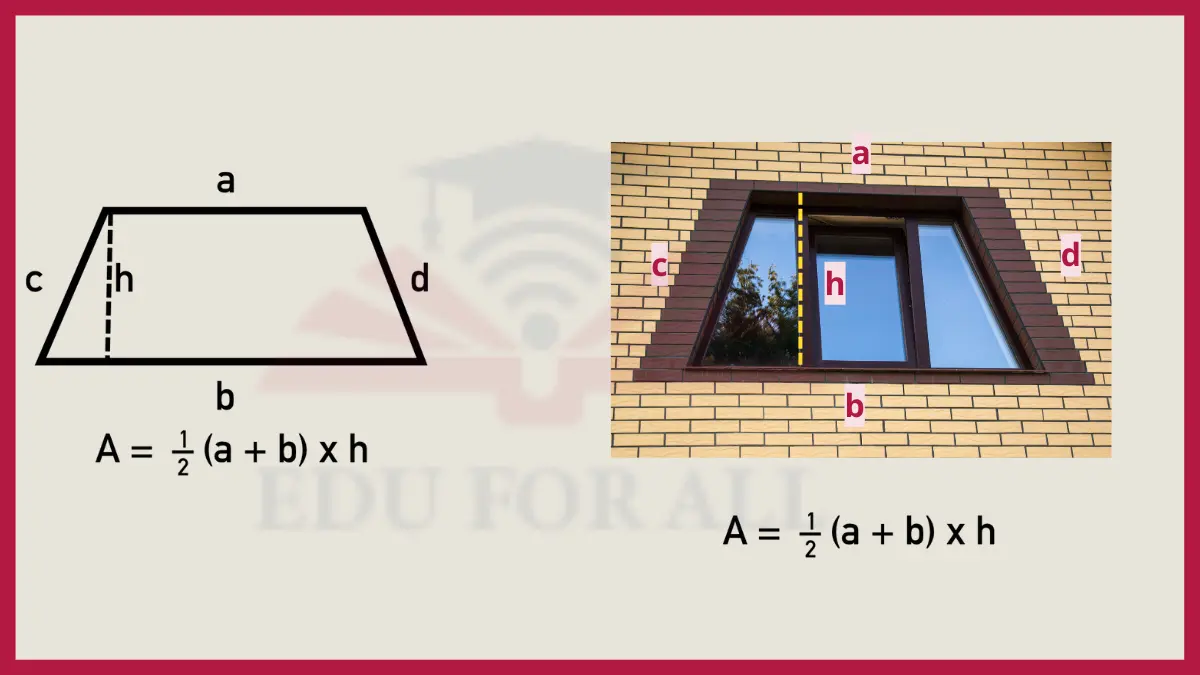
Used to determine the surface area of a trapezoidal roof.
Experiment: On paper, construct a trapezoid with straight sides and a set height. Use a ruler to carefully measure the lengths of the two parallel bases and the perpendicular height. Add the base measurements together, divide by 2, and then multiply by the height to calculate the total area of the trapezoid.
5. Parallelogram Area
To find the area of a parallelogram, multiply its base by its corresponding height: Area = Base x Height. For example, if a parallelogram has a base of 8 units and a height of 5 units perpendicular to that base, then its area would be 8 x 5 = 40 square units.
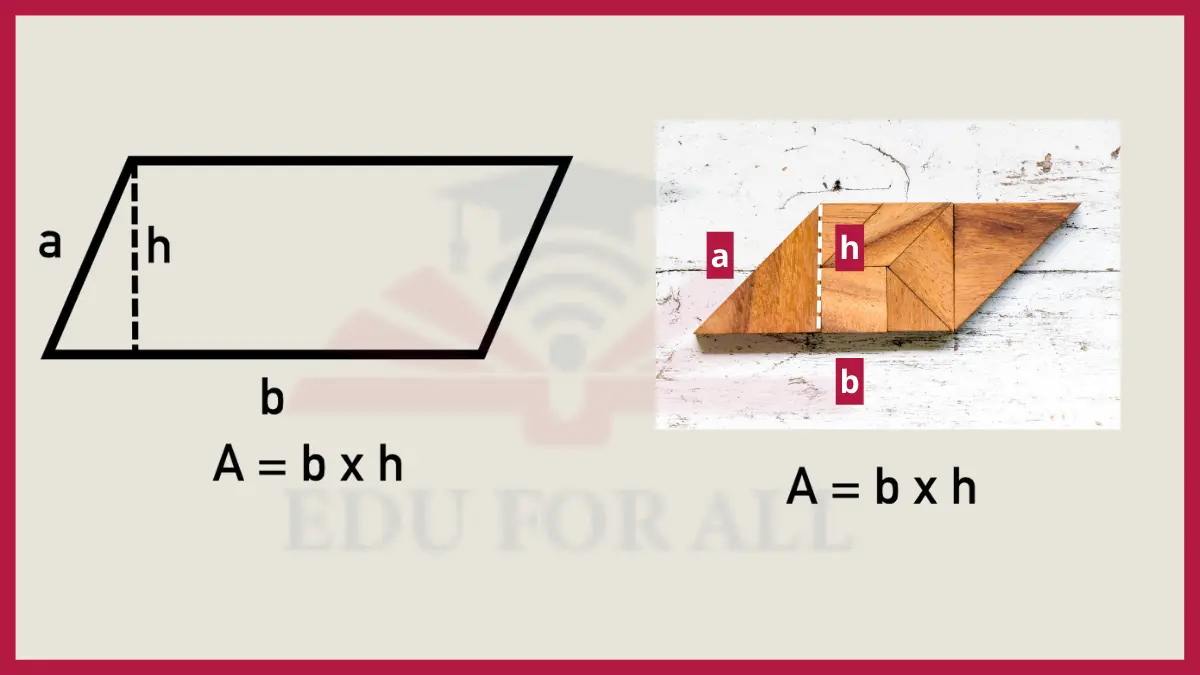
Used to determine the area of a parallelogram-shaped piece of land.
Experiment: Cut a parallelogram out of cardboard. Use a ruler to measure its base along one of the sides. Then draw in the corresponding height by making a line from the opposite corner that meets at 90 degrees. Multiply the base and height lengths to get the total area.
6. Ellipse Area
The area of an ellipse is calculated using the formula: Area = π x a x b, where a is half the length of the ellipse’s major axis and b is half the length of its minor axis.
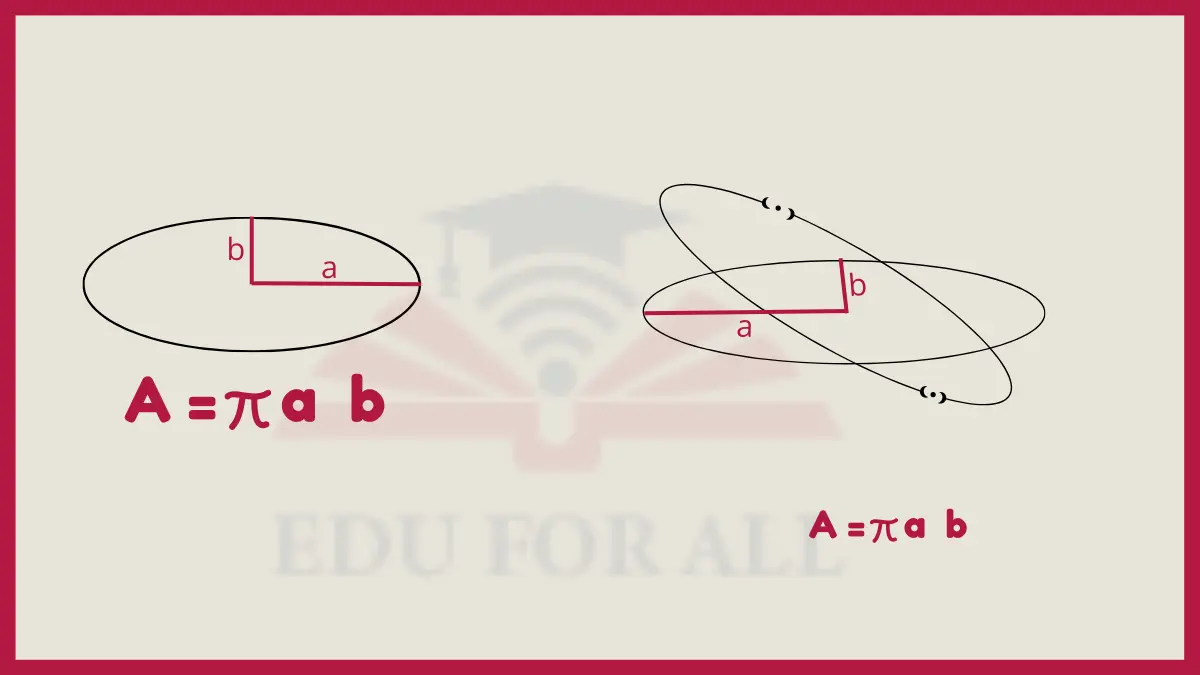
Used to determine the area of elliptical flower beds in a garden.
Experiment: Draw an ellipse on graph paper. Use a ruler to carefully measure the ellipse’s major axis (its longest width) and minor axis (its shortest width). Divide each measurement in half to get values for a and b. Multiply π, a and b together to calculate the total area.
7. Rhombus Area
To find the area of a rhombus, multiply the length of its two diagonals together and then divide by 2: Area = (d1 x d2) / 2. For example, if its diagonals are 8 units and 6 units long, the area would be (8 x 6) / 2 = 24 square units.
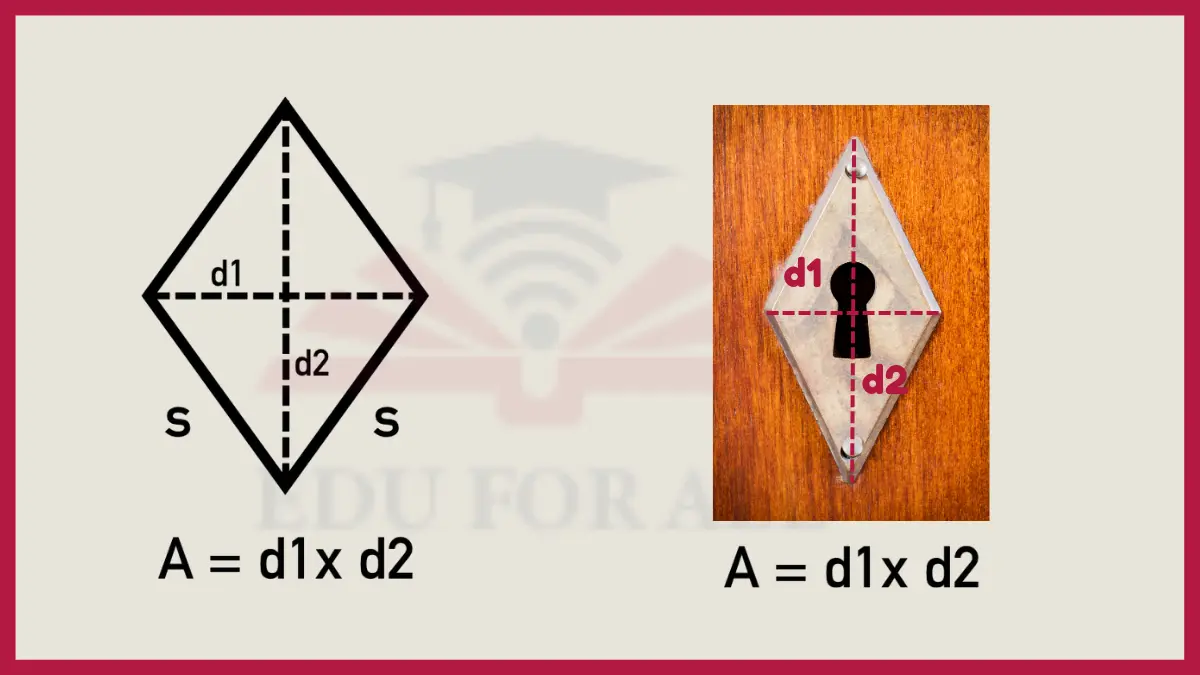
Used to determine the material needed for a rhombus-shaped sign.
Experiment: Draw a rhombus and use a ruler to measure the lengths of its two diagonals (the lines linking opposite corners). Multiply the diagonal lengths together, divide them by 2, and you’ll have the rhombus’ total area.
8. Sector Area
The area of a sector of a circle is found by the formula: Area = (θ / 360) x π x r2, where θ is the central angle of the sector in degrees, r is the radius of the circle.
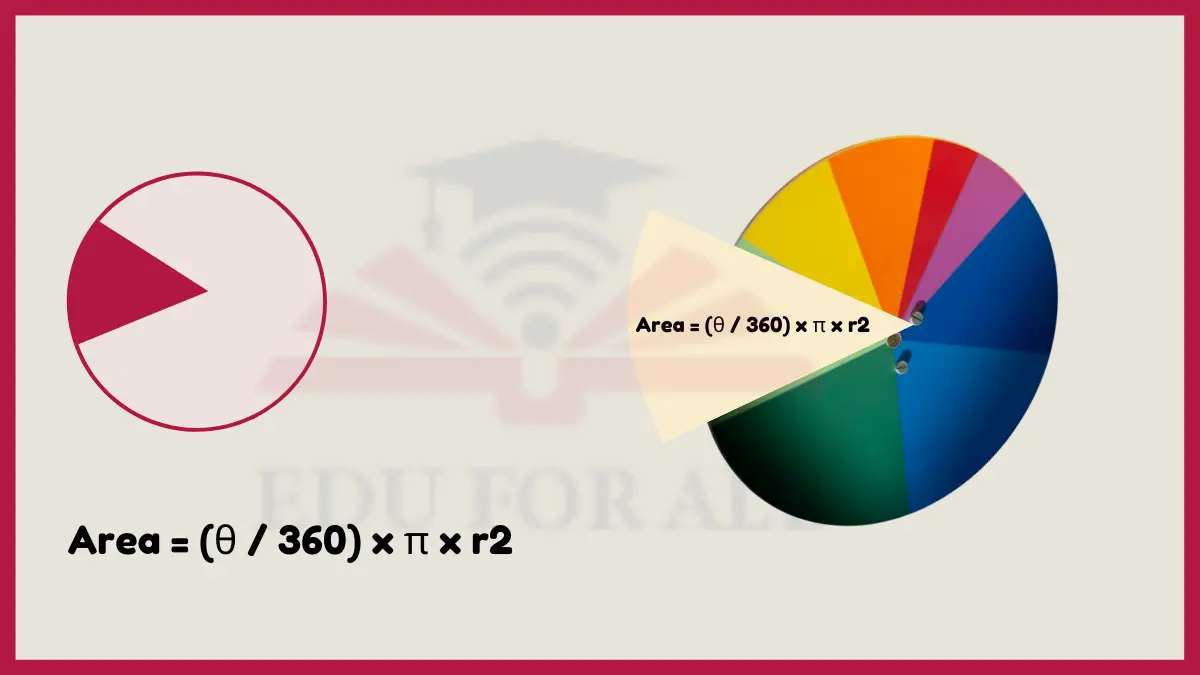
Used to determine the area of a sliced pizza.
Experiment: Use a protractor to carefully measure the central angle of a sector you’ve drawn from a circle with a set radius. Divide the central angle by 360. Multiply this by π, and then by the squared radius measurement to determine the sector area.
9. Hexagon Area
To calculate the area of a regular hexagon with side s, use the formula: Area = (3√3 / 2) x s2. For a hexagon with 4 unit long sides, this would be: Area = (3√3/2) x 42 = 24√3 sq. units.

Used to determine the amount of material needed for a hexagon-shaped floor tile.
Experiment: Draw a regular hexagon with all 6 equal sides. Use a ruler to measure the length s of one of the sides. Plug s into formula to find the hexagon’s total area.
10. Irregular Shape Area
To find the area of an irregular shape, divide it into basic shapes like triangles, rectangles, circles and trapezoids. Calculate each of their areas separately then add all those areas together.

Experiment: On graph paper, draw an irregular shape. Break it down into identifiable basic shapes. Use the appropriate area formula for each distinct shape. Sum the areas you calculated for all the pieces to determine the total area.
Also Read

