There are many examples of angles around us. A right angle forms a 90 degree corner. Carpenters use them to make square frames. Complementary angles add up to 90 degrees. Sailboat navigators measure these angles between the sky and horizon to chart direction.
Adjacent angles share a common side. Skaters use adjacent sidewalk angles already there to grind. These show angles categorized in math apply in real objects too. Buildings, maps, ramps – the shapes we use have angles from geometry. Simple angles make up big things in life.

Examples of Angles
Here are 12 examples of angles:
1: Right Angle
Right angle is the most common example of an angle. A right angle measures exactly 90 degrees. It forms a corner with two perpendicular lines intersecting at the 90 degree point.
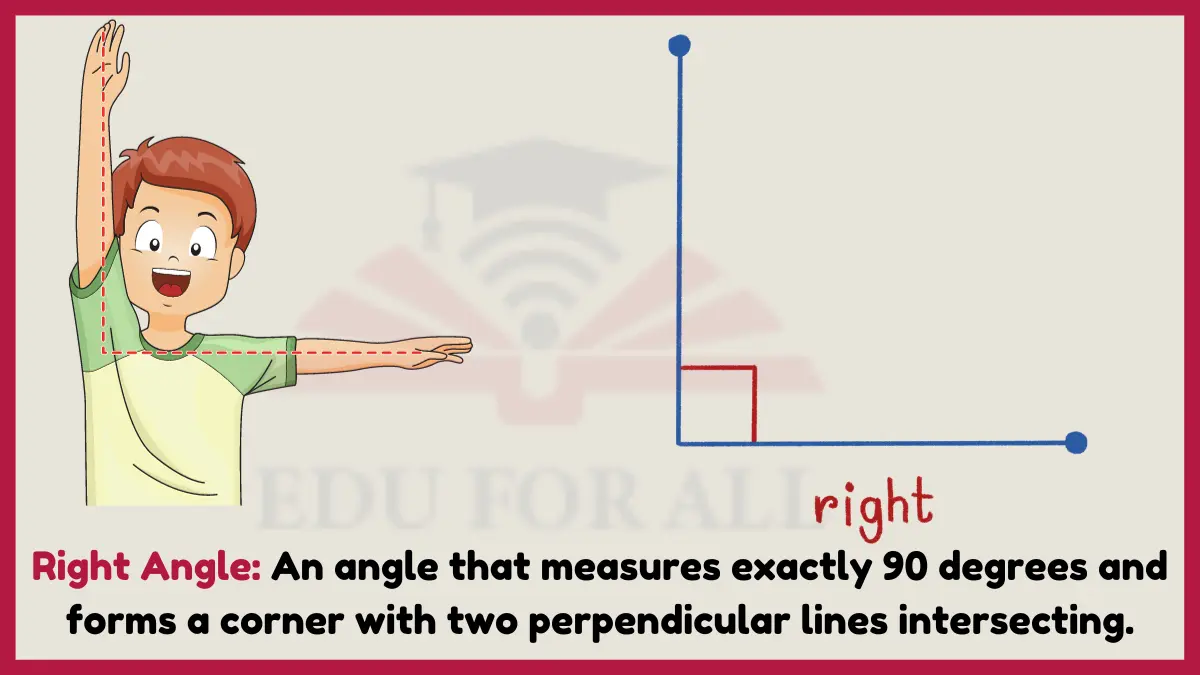
Right angles provide square, stable structure for construction. Carpentry uses right angles cutting trim, roofing, and flooring corners at precise 90 degrees. Engineers apply them designing machinery and parts with edges and joints meeting at 90 degree alignments.
Experiment: Use a protractor and ruler to draw, measure, and verify right angles of various sizes on paper. Construct 3D right angle corners out of Legos or cardboard.
2: Acute Angle
An acute angle measures less than 90 degrees. Sharp angles ranging anywhere between 0 and 89 degrees constitute acute angles.
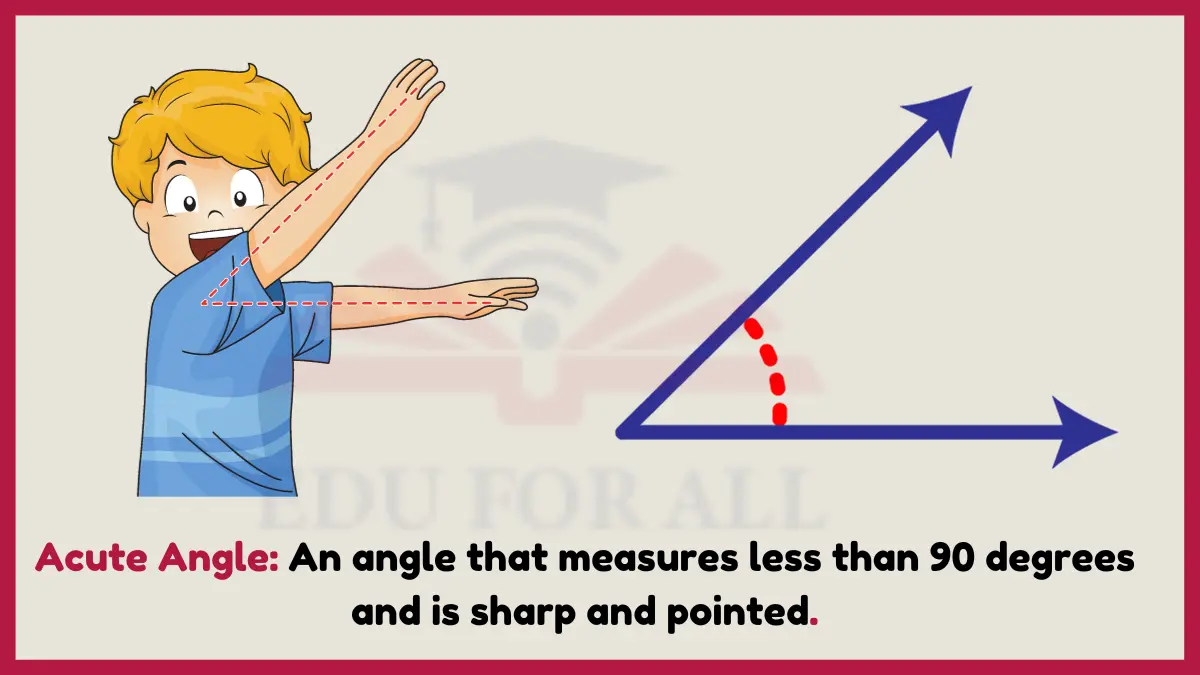
Acute angles enable pointed tips such as knife blades for precision cutting, arrowheads for flight, and shark teeth for tightly snagging prey with their narrow yet sturdy geometry. Photon beams also refract at calculated acute angles as they traverse materials.
Experiment: Identify numerous acute angles found around the classroom on books, tables, fixtures etc. Measure them with protractors and compare values.
3: Obtuse Angle
Obtuse angles span between 90 to less than 180 degrees. They form a wide spread rather than coming to a point or corner.

An obtuse bend exceeding 90 degrees allows flexible hinged joints in animal limbs to open wider using the expanded angle’s capacity. Sports like discuses and javelins similarly utilize wide obtuse arm extension for added performance.
Experiment: Position your arms to form obtuse angles. Estimate the angle with your eyes then use a protractor to measure it accurately. Explore modeling different obtuse openings with paper strips.
4: Straight Angle
A straight angle constitutes a single flat line measuring exactly 180 degrees. Side-by-side textbooks demonstrate straight 180 degree covers, as may long building walls or sighting tube transits.
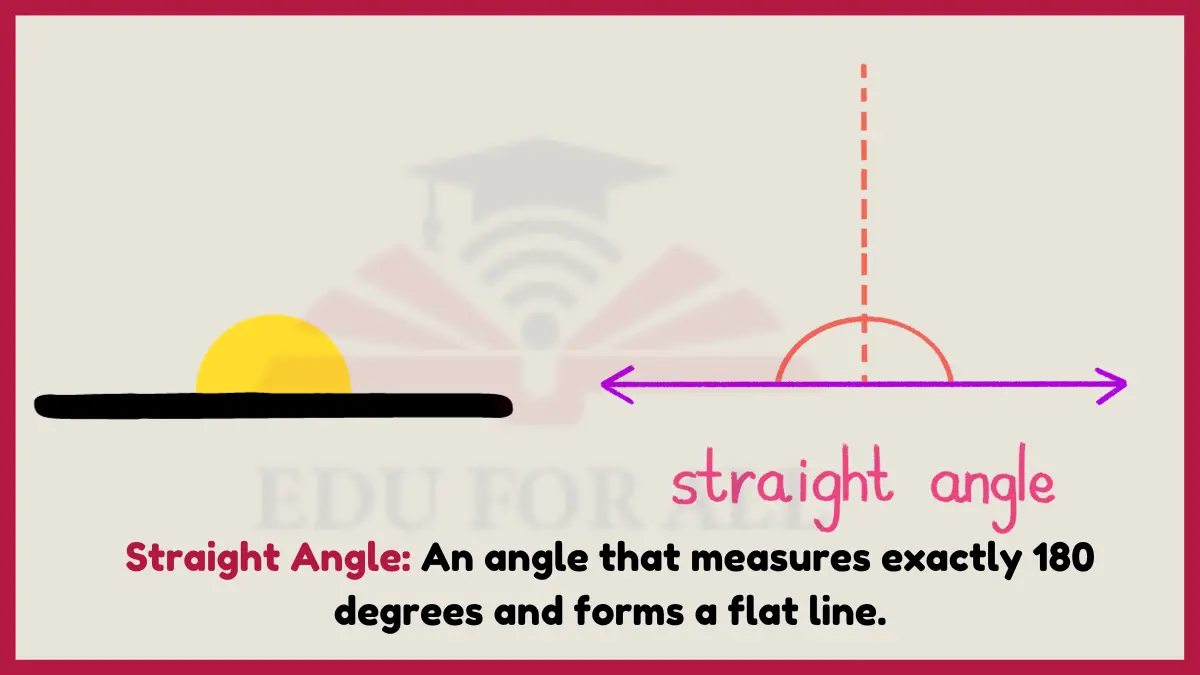
Surveyors align transit scopes to narrow straight angles sighting steady markers over long distances. Construction benefits from braced straight angle corner reinforcements and level foundation edging. Standing soldiers also form straight angles inspecting posture.
Experiment: Fold paper to align edges into various straight angles. Use a protractor to validate 180 degrees. Peer through cylindrical paper rolls as straight-angle sighting aids.
5: Reflex Angle
A reflex angle bends more than 180 degrees – sharply overextending until the lines fold backward.

Reflex angles enable complex bio-molecular structures like tangled protein folding to twist back beyond a straight line to achieve stabilized shapes. Tree climbing animals like pandas also utilize reflex angle limbs for flexible extended grasping and rotation.
Experiment: Position your arm to form a reflex angle above 180 degrees. Estimate the angle with your eyes then use a protractor to measure it accurately.
6: Perigon
A perigon constitutes a full circular 360 degree angle bounded by overlapping vertices that complete the loop.
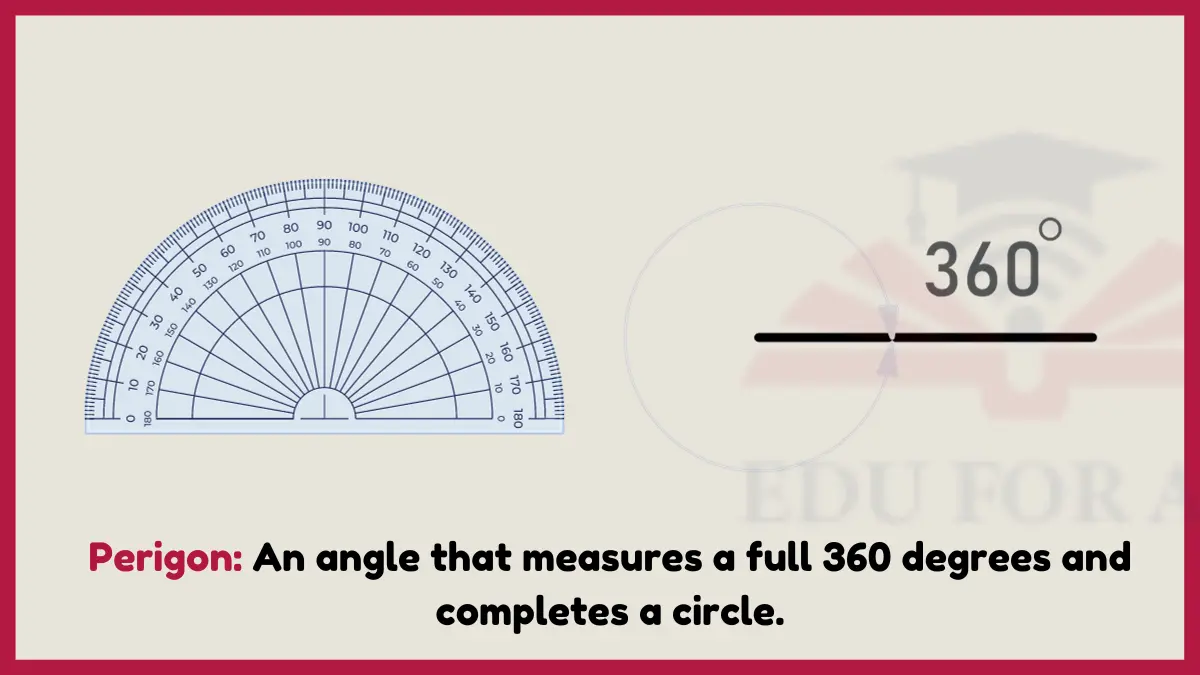
Perigon angles assist panoramic photographers in aligning sweeping 360 degree views into a single merged image. Radar arrays also rotate in full perigon circles continuously sweeping areas with radio waves.
Experiment: Tape paper ends together into a bracelet representing a perigon circle. Rotate and peer through the loop to estimate and validate the 360 angle.
7: Vertical Angles
Vertical angles reside opposite one another orientated as matching pairs across an intersection always equal in degrees.
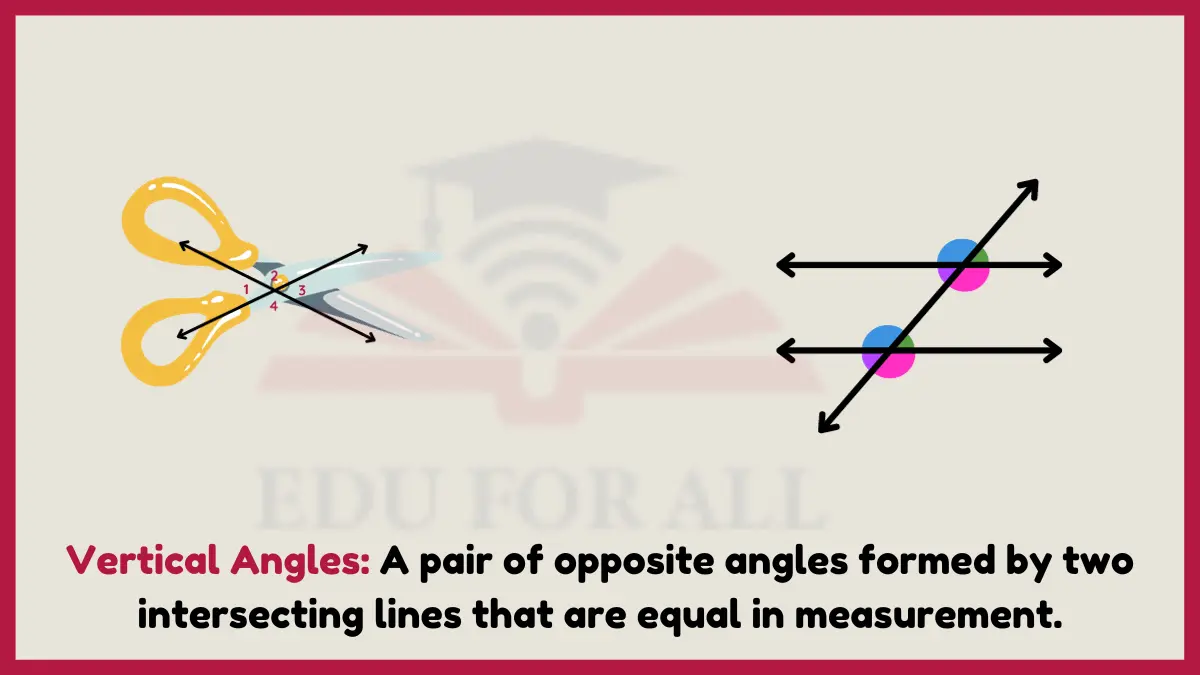
Carpenters construct building foundations using corresponding vertical 90 degree corner angles to square groundworks for level wall framing. Boomerangs also leverage mirrored vertical angles so aerodynamics return them to flight paths.
Experiment: Draw perpendicular lines on paper. Determine if the 4 angles formed are equivalent vertical angles using measurement. Construct Lego structures with equivalent vertical angles in foundations.
8: Alternate Angles
Alternate angles are non-adjacent angles created by a transversal line cutting across parallel horizontal lines, positioned alternative to each other yet equal in measurement.
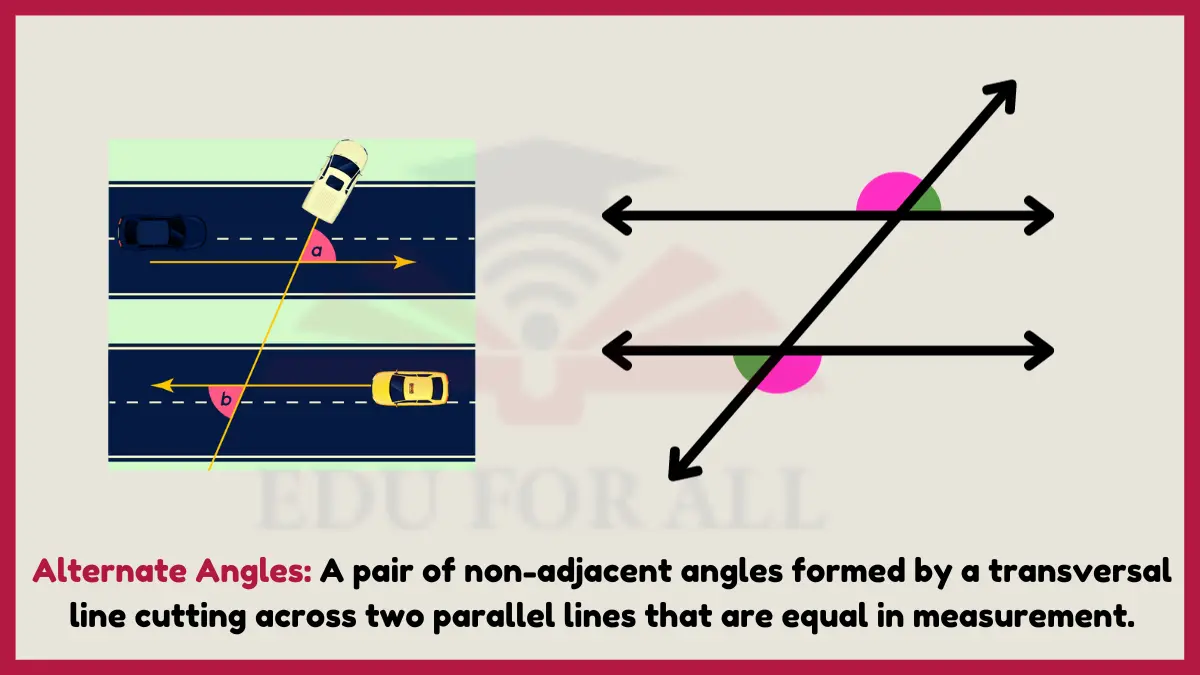
Railroad engineers carefully survey and map out track alignments utilizing alternate angles so branching lines remain safely parallel rather than interfering. Alternate angles also allow power lines to traverse existing infrastructure without interference.
Experiment: Draw 2 parallel lines on paper crossed by a transversal. Determine if specific non-adjacent angles formed are equivalently alternate. Shift the transversal to recreate alternate angles of different degree.
9: Complementary Angles
Complementary angles constitute a pair that adds up to exactly 90 degrees, forming the two components of a right angle together.
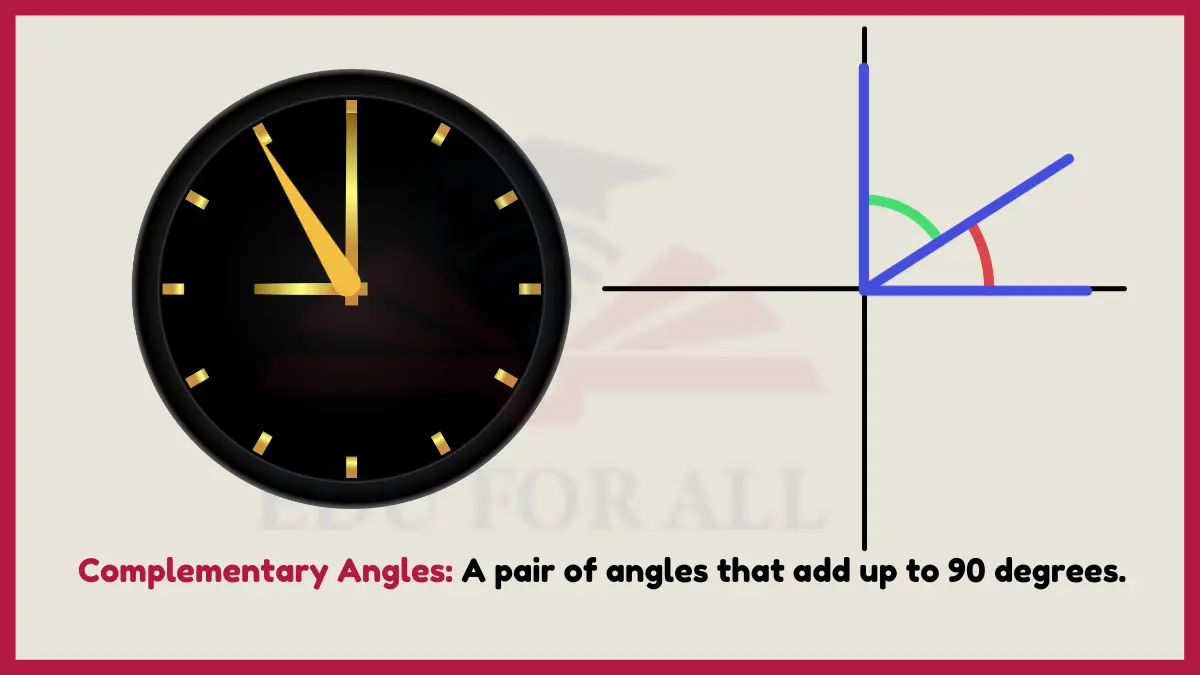
Navigators utilize sextant measurements establishing complementary angles between the horizon and celestial objects like stars to triangularly calculate position coordinates while traversing oceans. Complementary camera shutter mechanisms also use paired angles that fully open and close apertures.
Experiment: Use a protractor to draw 2 angles on paper that combine to equal 90 degrees. Validate they are complementary angles by addition. Shift one angle larger while making the paired one smaller yet still complementary.
10: Supplementary Angles
Supplementary angles sum up to exactly 180 degrees in a continuous straight line rather than 90 degree right angles.
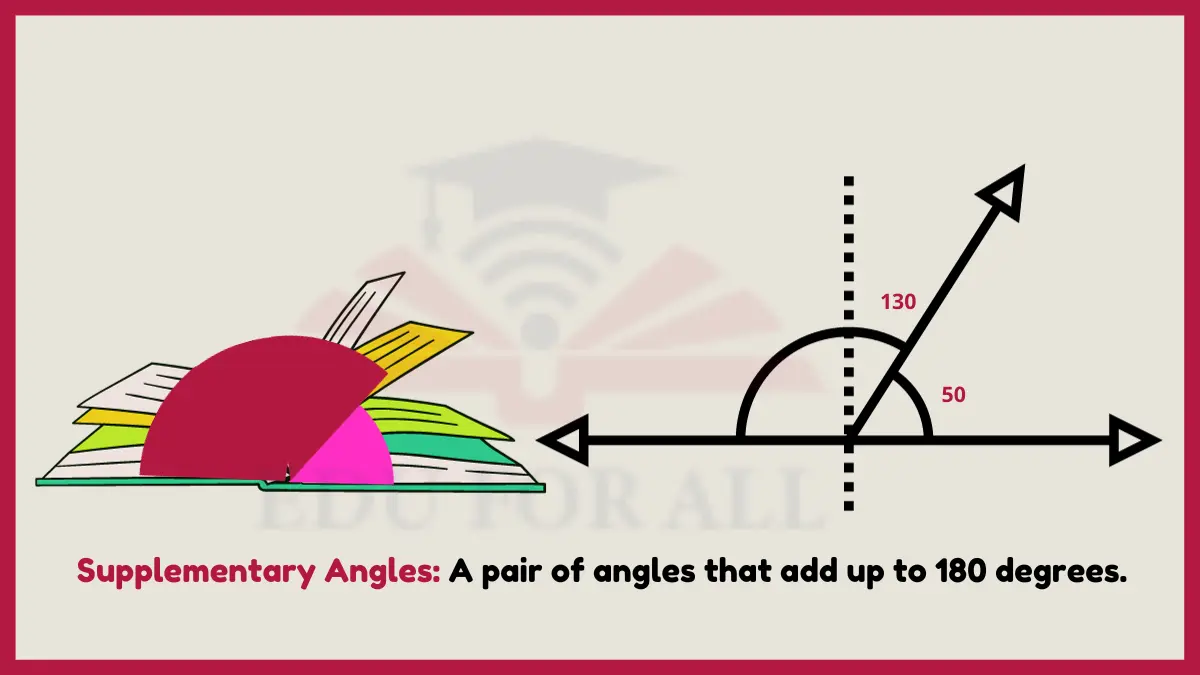
Contortionists and gymnasts often bend into poses that extend supplementary body angles passing through regular joint alignments. Collapsible tent poles also utilize supplementary angles to quickly pop segments into a rigid straight linker.
Experiment: Construct 2 equal length sticks with a pivot joint. Manipulate to identify supplementary stick alignments at 180, 120 and 90 degree arrangements.
11: Congruent Angles
Congruent angles match precisely, equivalent in their angle measure just as congruent sides are exactly equal lengths.

Aircraft wings rely on properly congruent wing flap angles during takeoff and landing to generate balanced lift forces that keep planes stable. Student model gliders also apply matched left and right-side wing angles.
Experiment: Copy an angle template outline to cut and test paper angles for congruency using tracing and overlays to validate.
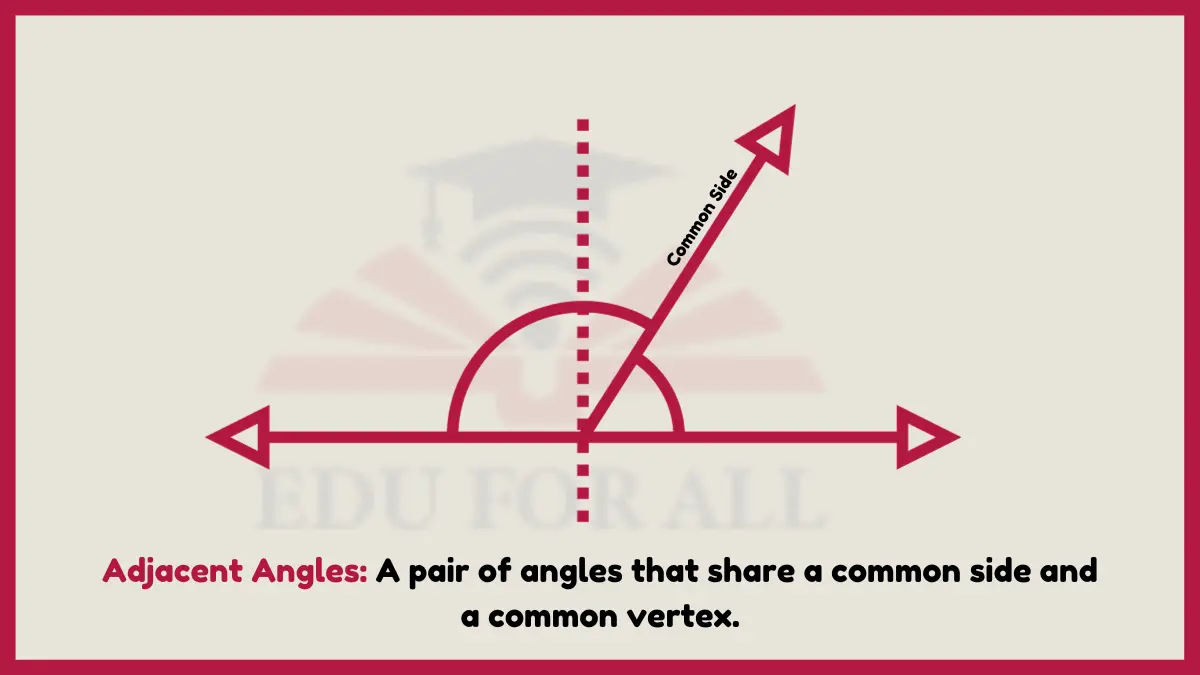
12: Adjacent Angles
Adjacent angles directly connect sharing a common vertex and side, adjacent to rather than across from each other.
Skateboarders scope out adjacent complementary ground inclines of driveways and curbs to grind diagonal edges, utilizing the matched angles already intrinsic to the structures.
Experiment: Outline a simple house with corners and peaked roof on paper. Determine if markings of walls and roof edges create adjacent vs. vertical surface angles.
Also Read





